Chủ đề diện tích S xq hình trụ: Diện tích xq hình trụ là một trong những đặc điểm cần thiết của hình trụ, được chấp nhận tao tính được phần diện tích S xung quanh phía bên ngoài của hình trụ. Đây là một trong những công thức đo lường riêng biệt và đặc biệt hữu ích trong những việc toán học tập và vô thực tiễn. Việc biết diện tích S xq hình trụ canh ty tất cả chúng ta làm rõ rộng lớn về hình dạng và những đặc điểm của hình trụ.
Diện tích xq hình trụ được xem như vậy nào?
Để tính diện tích S xung xung quanh và diện tích S toàn phần của một hình trụ, tao dùng những công thức sau:
1. Diện tích xung xung quanh (Sxq) của hình trụ:
- Công thức: Sxq = 2 * π * r * h
- Trong đó: r là nửa đường kính lòng của hình trụ, h là độ cao của hình trụ
2. Diện tích toàn phần (Stp) của hình trụ:
- Công thức: Stp = Sxq + 2 * Sđáy
- Trong đó: Sđáy là diện tích S lòng của hình trụ
- Diện tích lòng (Sđáy) sở hữu công thức không giống nhau tùy nằm trong vô hình dạng lòng của hình trụ (ví dụ: hình trụ tròn trĩnh, hình trụ vuông, hình trụ chữ nhật).
Ví dụ: Cho một hình trụ tròn trĩnh sở hữu nửa đường kính lòng r = 4 centimet và độ cao h = 6 centimet.
- Để tính diện tích S xung xung quanh (Sxq):
Sxq = 2 * π * r * h = 2 * 3.14 * 4 * 6 = 150.72 cm2
- Để tính diện tích S toàn phần (Stp):
Trước tiên, tao cần thiết tính diện tích S lòng (Sđáy) của hình trụ, với công thức:
Sđáy = π * r2 = 3.14 * 4^2 = 50.24 cm2
Bạn đang xem: công thức tính diện tích xung quanh của hình trụ
Sau ê, vận dụng công thức diện tích S toàn phần:
Stp = Sxq + 2 * Sđáy = 150.72 + 2 * 50.24 = 251.trăng tròn cm2
Vậy, diện tích S xung xung quanh (Sxq) của hình trụ là 150.72 cm2 và diện tích S toàn phần (Stp) là 251.trăng tròn cm2.
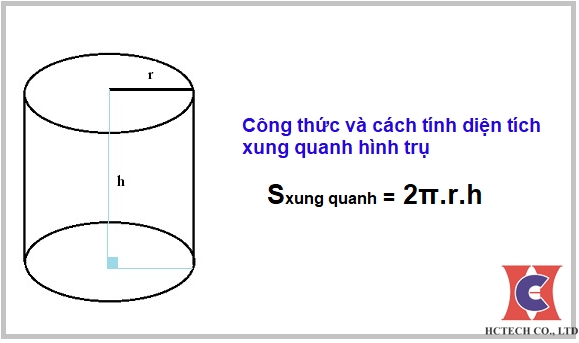
Diện tích xung xung quanh hình trụ sở hữu công thức đo lường như vậy nào?
Diện tích xung xung quanh của một hình trụ hoàn toàn có thể được xem vị công thức sau: Sxq = 2πrh, vô ê π là số pi, r là nửa đường kính lòng của hình trụ, h là độ cao của hình trụ.
Ví dụ, fake sử nửa đường kính lòng của hình trụ là 4 centimet và độ cao của chính nó là 6 centimet. Ta hoàn toàn có thể tính diện tích S xung xung quanh vị công thức trên: Sxq = 2π(4)(6) = 2π(24) = 48π (cm²).
Vậy diện tích S xung xung quanh của hình trụ này là 48π cm².
Lưu ý rằng đơn vị chức năng diện tích S (cm²) tùy thuộc vào đơn vị chức năng được dùng cho tới nửa đường kính và độ cao của hình trụ.
Diện tích toàn phần của hình trụ được xem bằng phương pháp nào?
Để tính diện tích S toàn phần của một hình trụ, tao dùng công thức:
S_toan_phan = S_xq + 2 * S_day
Trong đó:
- S_xq là diện tích S xung xung quanh hình trụ, được xem vị công thức: S_xq = 2 * π * r * h, với r là nửa đường kính lòng của hình trụ và h là độ cao của hình trụ.
- S_day là diện tích S lòng của hình trụ, được xem vị công thức: S_day = π * r^2, với r là nửa đường kính lòng của hình trụ.
Ví dụ: Giả sử tao sở hữu một hình trụ với nửa đường kính lòng r = 4 centimet và độ cao h = 6 centimet. Để tính diện tích S toàn phần của hình trụ này, tao triển khai theo đòi công việc sau:
1. Tính diện tích S xung xung quanh hình trụ: S_xq = 2 * π * r * h = 2 * π * 4 * 6 = 48π cm^2 (kết trái khoáy xấp xỉ)
2. Tính diện tích S lòng của hình trụ: S_day = π * r^2 = π * 4^2 = 16π cm^2 (kết trái khoáy xấp xỉ)
3. Tính diện tích S toàn phần của hình trụ: S_toan_phan = S_xq + 2 * S_day = 48π + 2 * 16π = 80π cm^2 (kết trái khoáy xấp xỉ)
Vậy diện tích S toàn phần của hình trụ vô ví dụ này là 80π cm^2 (kết trái khoáy xấp xỉ).

Toán học tập lớp 9 Chương 4 Bài 1 Diện tích xung xung quanh và thể tích hình trụ Tiết 1
Toán học: Quý Khách ham muốn mày mò vẻ đẹp nhất toán học? Hãy nằm trong coi đoạn phim này nhằm mày mò những công thức quy tắc tính thú vị, những mày mò mới mẻ về toán và những phần mềm thú vị của chính nó vô cuộc sống đời thường hằng ngày.
Có từng nào loại diện tích S vô hình trụ và bọn chúng sở hữu công thức tính riêng lẻ không?
Trong hình trụ, tất cả chúng ta sở hữu nhì loại diện tích S, này là diện tích S xung xung quanh và diện tích S toàn phần. Cả nhì loại diện tích S này được xem theo đòi công thức riêng lẻ.
1. Diện tích xung xung quanh (Sxq) là phần diện tích S xung quanh phía bên ngoài của hình trụ. Để tính diện tích S xung xung quanh, tất cả chúng ta dùng công thức sau: Sxq = 2 * π * r * h, vô ê r là nửa đường kính của lòng hình trụ và h là độ cao của hình trụ.
2. Diện tích toàn phần (Stp) là tổng thể của diện tích S xung xung quanh và diện tích S lòng của hình trụ. Để tính diện tích S toàn phần, tất cả chúng ta dùng công thức sau: Stp = Sxq + 2 * Sđáy. Công thức này hoàn toàn có thể tổng quát lác rộng lớn, tùy nằm trong vô hình dạng của lòng hình trụ. Đối với hình trụ tròn trĩnh, diện tích S lòng (Sđáy) được xem vị π * r^2, vô ê r là nửa đường kính lòng của hình trụ.
Vì vậy, sở hữu nhì loại diện tích S vô hình trụ và bọn chúng sở hữu công thức tính riêng lẻ.
Nếu biết nửa đường kính lòng và độ cao của hình trụ, thực hiện thế này nhằm tính diện tích S toàn phần của nó?
Để tính diện tích S toàn phần của hình trụ, tao hoàn toàn có thể tuân theo công việc sau:
Bước 1: Xác quyết định nửa đường kính lòng (r) và độ cao (h) của hình trụ.
Bước 2: Tính diện tích S xung xung quanh (Sxq) của hình trụ vị công thức:
Sxq = 2 * π * r * h
Bước 3: Tính diện tích S những lòng (Sđáy) của hình trụ vị công thức:
Sđáy = π * r^2
Bước 4: Tính diện tích S toàn phần (Stp) của hình trụ vị công thức:
Stp = Sxq + 2 * Sđáy
Ví dụ: Cho một hình trụ sở hữu nửa đường kính lòng r = 4 centimet và độ cao h = 6 centimet.
Tính diện tích S toàn phần của hình trụ:
Bước 1: r = 4 centimet, h = 6 cm
Bước 2: Tính diện tích S xung quanh:
Sxq = 2 * π * r * h = 2 * 3.14 * 4 * 6 = 150.72 cm^2
Bước 3: Tính diện tích S đáy:
Sđáy = π * r^2 = 3.14 * 4^2 = 50.24 cm^2
Bước 4: Tính diện tích S toàn phần:
Stp = Sxq + 2 * Sđáy = 150.72 + 2 * 50.24 = 251.trăng tròn cm^2
Vậy diện tích S toàn phần của hình trụ là 251.trăng tròn cm^2.
Xem thêm: tắc kè kêu 4 tiếng
_HOOK_
Hình trụ Diện tích xung xung quanh và thể tích của hình trụ Bài 1 Toán học tập 9 HAY NHẤT
Hình trụ: Hình trụ là một trong những trong mỗi định nghĩa cơ phiên bản vô hình học tập không khí. Hãy coi đoạn phim này nhằm làm rõ rộng lớn về cấu tạo và đặc điểm của hình trụ, và những phần mềm thú vị nhưng mà tất cả chúng ta hoàn toàn có thể dùng vô thực tiễn.
Tính diện tích S xung xung quanh hình trụ nếu như vẫn biết nửa đường kính và độ cao.
Để tính diện tích S xung xung quanh hình trụ nếu như vẫn biết nửa đường kính và độ cao, tao sở hữu công thức:
Diện tích xung xung quanh hình trụ = 2 * π * r * h
Trong đó:
- π là độ quý hiếm xấp xỉ của số Pi, có mức giá trị là khoảng chừng 3.14.
- r là nửa đường kính lòng của hình trụ.
- h là độ cao của hình trụ.
Cách tính diện tích S xung xung quanh hình trụ sẽ tiến hành triển khai như sau:
1. Gán độ quý hiếm cho tới nửa đường kính lòng (r) và độ cao (h) của hình trụ.
2. Tính tích của 2, π, r và h.
3. Nhân sản phẩm kể từ bước 2 với 2.
4. Nhân sản phẩm kể từ bước 3 với độ quý hiếm của Pi (khoảng 3.14).
5. Kết trái khoáy nhận được đó là diện tích S xung xung quanh hình trụ.
Ví dụ:
Giả sử hình trụ sở hữu nửa đường kính lòng r = 4 centimet và độ cao h = 6 centimet.
- sít dụng công thức: Diện tích xung xung quanh hình trụ = 2 * π * r * h.
- Gán độ quý hiếm vô công thức: Diện tích xung xung quanh hình trụ = 2 * 3.14 * 4 * 6.
- Tính toán: Diện tích xung xung quanh hình trụ = 150.72 (khoảng).
Vậy, diện tích S xung xung quanh hình trụ vô tình huống này là khoảng chừng 150.72 (khoảng).
Tính diện tích S xung xung quanh hình trụ nếu như biết diện tích S lòng và độ cao.
Để tính diện tích S xung xung quanh của một hình trụ, tao cần phải biết diện tích S lòng và độ cao của hình trụ.
Bước 1: Thứ nhất, tao xác lập diện tích S lòng của hình trụ. Diện tích lòng được xem vị công thức của diện tích S hình dạng lòng ứng, ví như hình trụ thì diện tích S lòng là
Sđáy = π * r^2
Trong ê, r là nửa đường kính của lòng.
Bước 2: Tiếp theo đòi, tao tính diện tích S xung xung quanh. Diện tích xung xung quanh của hình trụ là phần diện tích S xung quanh phía bên ngoài của hình trụ. Công thức tính diện tích S xung xung quanh của hình trụ là
Sxq = 2 * π * r * h
Trong ê, r là nửa đường kính của lòng và h là độ cao của hình trụ.
Ví dụ: Giả sử diện tích S lòng của một hình trụ là trăng tròn cm^2 và độ cao là 10 centimet.
Bước 1: Diện tích lòng là Sđáy = trăng tròn cm^2.
Bước 2: Diện tích xung xung quanh là Sxq = 2 * π * r * h = 2 * π * √(20/π) * 10 = 40√(20/π) cm^2 (kết trái khoáy hoàn toàn có thể được sản xuất tròn).
Vậy, diện tích S xung xung quanh của hình trụ nếu như biết diện tích S lòng là trăng tròn cm^2 và độ cao là 10 centimet là 40√(20/π) cm^2.
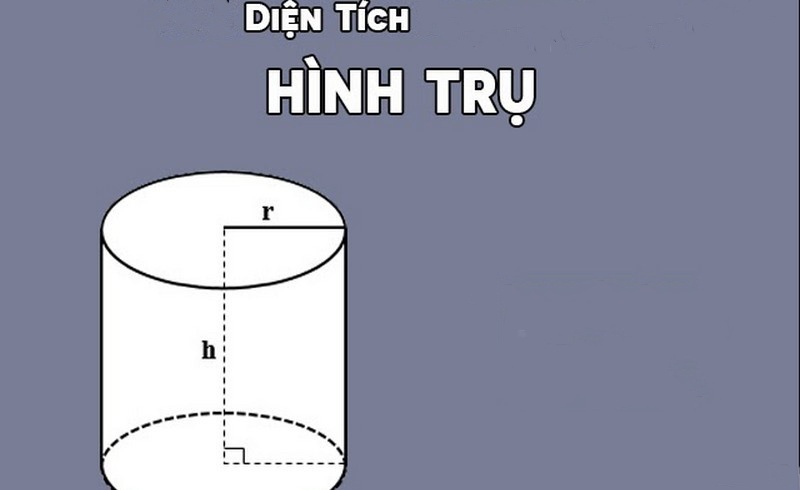
Có những tình huống này nhưng mà diện tích S xung xung quanh và diện tích S toàn phần của hình trụ vị nhau?
Diện tích xung xung quanh và diện tích S toàn phần của một hình trụ đều nhau trong những tình huống sau đây:
- Khi độ cao của hình trụ vị 0: Nếu độ cao của hình trụ là 0, diện tích S xung xung quanh và diện tích S toàn phần của hình trụ tiếp tục vị 0 vì thế không tồn tại mặt phẳng này tồn bên trên.
- Khi độ cao của hình trụ vị ấn quyết định số hợp ý lý: Nếu độ cao của hình trụ được lựa chọn sao cho tới tổng của độ cao và nửa đường kính lòng là một trong những độ quý hiếm phù hợp, diện tích S xung xung quanh và diện tích S toàn phần hoàn toàn có thể đều nhau.
Ví dụ: Xét hình trụ sở hữu nửa đường kính lòng r và độ cao h. Khi r + h = một độ quý hiếm thắt chặt và cố định như π, diện tích S xung xung quanh và diện tích S toàn phần của hình trụ tiếp tục đều nhau.
Tuy nhiên, tình huống này sẽ không vận dụng cho tới toàn bộ những mô hình trụ nhưng mà chỉ vận dụng cho tới một vài tình huống ví dụ. Để đo lường diện tích S xung xung quanh và diện tích S toàn phần của hình trụ, tao cần phải biết công thức tính diện tích S của từng loại diện tích S.
Xem thêm: xoay người chợt thức giấc
Diện tích xung xung quanh hình trụ tùy thuộc vào những nguyên tố nào?
Diện tích xung xung quanh của hình trụ tùy thuộc vào phụ thân nguyên tố đó là nửa đường kính lòng (r), độ cao (h), và hằng số π (pi). Công thức nhằm tính diện tích S xung xung quanh của hình trụ là: Sxq = 2πrh. Trong số đó, π là hằng số PI, có mức giá trị xấp xỉ là 3.14. Bán kính lòng (r) là khoảng cách kể từ trung tâm lòng của hình trụ cho tới một điểm bên trên đàng viền lòng. Chiều cao (h) là khoảng cách kể từ mặt mày lòng hình trụ cho tới mặt mày đỉnh của hình trụ.
Tại sao diện tích S xq hình trụ được xem vị công thức 2 * π * r * h?
Diện tích xung xung quanh (xq) của một hình trụ được xem vị công thức 2 * π * r * h vì thế công thức này đo lường diện tích S của hình trụ bao hàm phần diện tích S xung quanh phía bên ngoài hình trụ.
Trong công thức này, π biểu thị cho tới số Pi (khoảng 3.14159) là một trong những hằng số được dùng nhằm đo lường diện tích S những hình trụ, và r biểu thị nửa đường kính lòng của hình trụ.
Hơn nữa, h biểu thị cho tới độ cao của hình trụ. Khi nhân r và h, tao tính được diện tích S xq của hình trụ.
Công thức này cũng hoàn toàn có thể được coi như là sự việc phó nhau thân thiết diện tích S toàn phần (được tính vị công thức 2 * π * r * (r + h)) và diện tích S lòng (được tính vị công thức π * r^2).
Tuy nhiên, cần thiết cảnh báo rằng công thức này chỉ vận dụng cho tới hình trụ và ko vận dụng cho những hình khác ví như hình cầu hoặc hình nón.
_HOOK_











Bình luận